核心:图卷积
在计算机视觉领域,Convolutional Neural Network(CNN)已经取得了巨大成就,主要针对Euclidean Structure的数据(图像属此类型)。
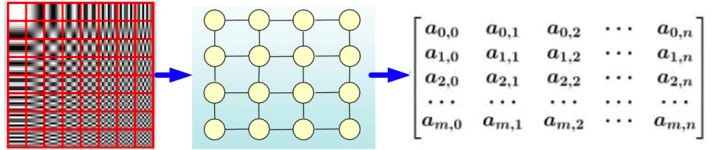
在Topological Structure(拓扑结构)数据中,相应的工具则是Graph Convolutional Network,可以应对更广义的结构数据。
GCN在ICLR 2017由T.Kipf, M.Welling正式提出(Semi-supervised Classification with Graph Convolutional Networks)。
先介绍一下图的基础知识。对于一个图:
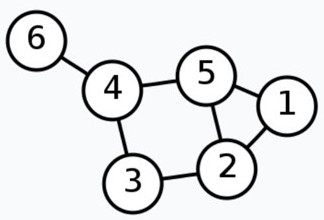
对应的数学表示为:
| Degree Matrix | Adjacency Matrix | Laplacian Matrix |
|---|---|---|
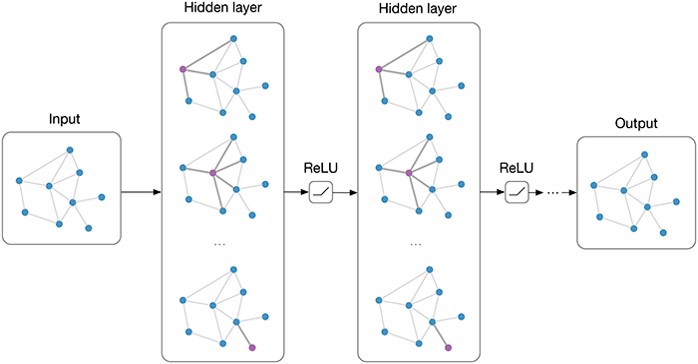
在GCN文中一开始便给出了核心,每两层直接的递推公式:
其中,是加上单位对角矩阵;是相应的度;为第层以各节点特征为行向量的矩阵(为输入);为权重矩阵,每层不同,是训练最终要得到的参数;是激活函数。
图卷积的来龙
我看到卷积公式之后,内心是崩溃的:为什么是这样一个公式,有什么道理吗?总不能是试来的吧?
抱着为什么的疑问,我对其来龙进行了简要的学习,这个过程还是蛮有意思的。下面是一个简要介绍,省略了数学的性质和推导,主要看中心思想。
众所周知,卷积是信号处理中的概念,与Fourier transform息息相关。GCN的概念也是从此推广而来。
图上的傅立叶变换
首先,图的Laplacian matrix 是半正定对称矩阵,利用其性质,可以进行矩阵分解
其中,是的个特征值组成的对角阵,是列向量为单位特征向量的矩阵。
因为是正交矩阵,有,所以有:
如何利用包含图结构的,和代表其特性的的和推导出图卷积的过程?
故事要从Fourier transform说起。傅立叶正变换:
公式很复杂,这里只说它的思想。傅立叶变换用形象一些的图表示为:
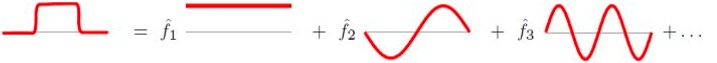
傅立叶逆变换,就是上图的逆向过程:
从物理角度理解傅里叶变换是以一组特殊的函数为正交基,对原函数进行线性变换,物理意义便是原函数在各组基函数的投影。这跟拉普拉斯矩阵的特征值分解有相同的本质。
如果将和看成时间信号,就可以套用傅里叶变换了。
类推Topological Graph上的傅立叶变换:
矩阵形式为
具体来说,就是
其中,是拓扑图中第n个节点的特征,是在特征值的域上的特征。
相应的逆变换为:
图上的卷积
傅里叶卷积:
推广到图卷积:
矩阵形式
设计核函数 为
则有
- 可以看出,最终的计算公式具有Spatial Localization
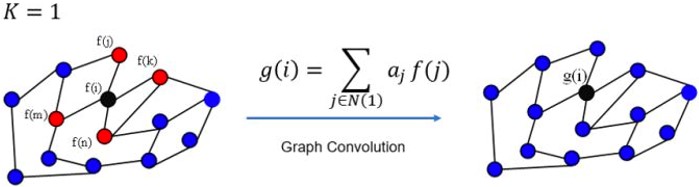

再结合是拉普拉斯矩阵的一种变形。所以,就不难理解了。
图卷积的应用
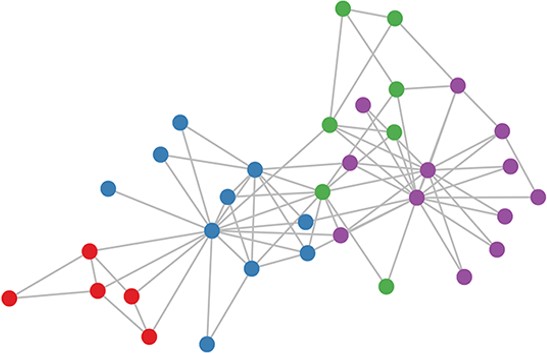
原文例:聚类

上图是一个社交网络(空手道俱乐部),节点表示成员的特征,边表示有社交关系,颜色代表了他们所属的小团体。不依靠节点的特征,只通过图,在随机初始化权重之后,经过两次前向传播,可以大致将成员分对。
原文例:半监督学习
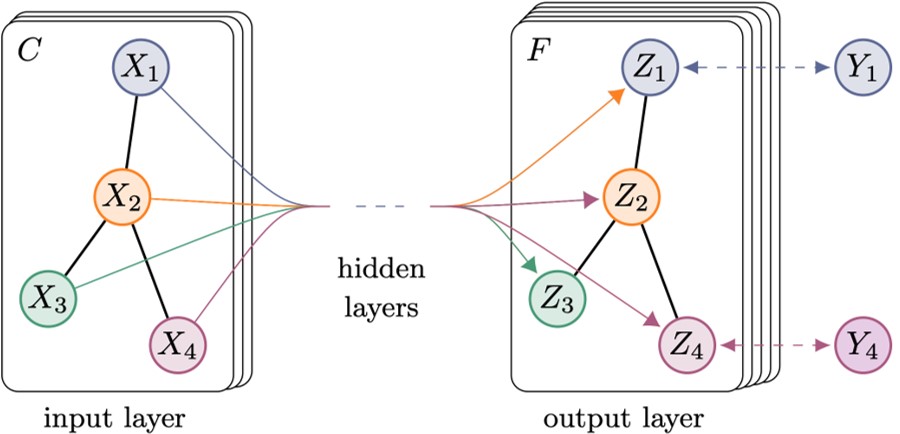
每类只只标记一个样本(图例是四类),将网络最终的输出做训练,即只对这四个样本做训练。剩下的样本在训练完成之后的输出即是预测。
视频动作识别
Wang, Xiaolong, and Abhinav Gupta. “Videos as Space-Time Region Graphs.” ECCV, 2018).
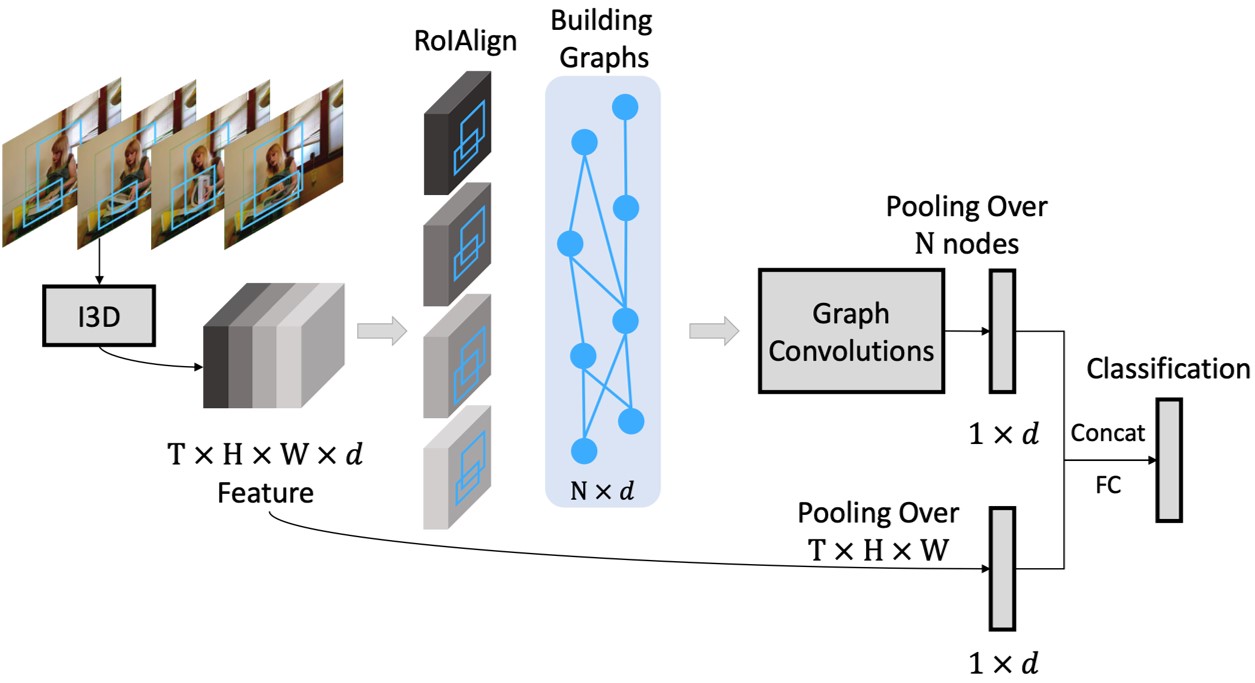
在前向传播的过程中,插入GCN模块。如图例,对连续四帧监测到的目标,建立图。可以将目标之间的关联信息加以利用,增强目标识别的效果。